Edit

Validation Schemes

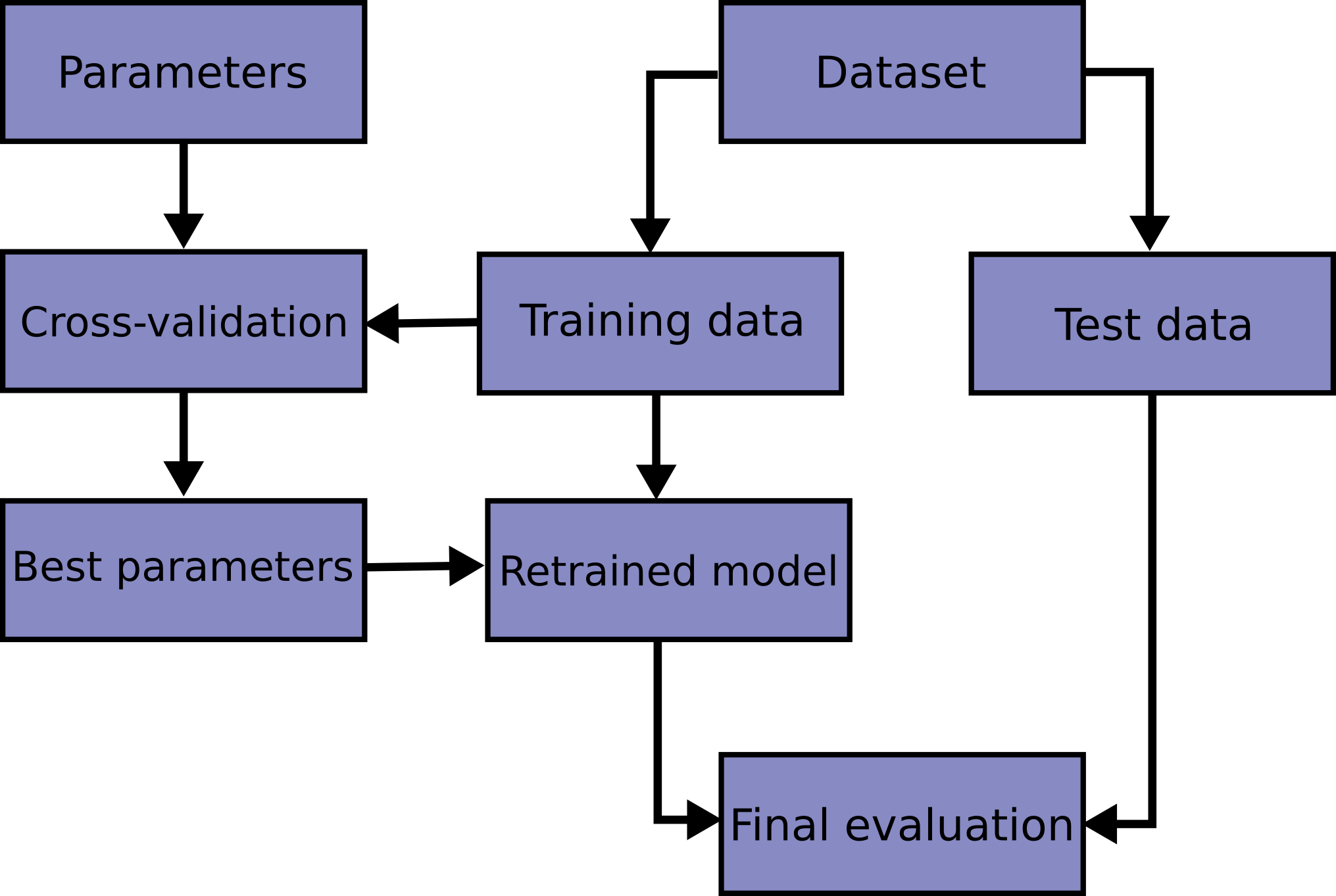
• Never use data you train on to measure the quality of your model (resubstitution).
  • As the model becomes more computational, the variance (dispersion) of the estimate increases, but bias decreases.
  • Overfitting arises due to the fact that the training set is memorized completely instead of generalizing.
  • This effect is only visible when the same estimator is run on similar data other than training.
• Hold out part of the available data as a test set.
  • There is still a risk of overfitting because the parameters can be tweaked until the estimator performs optimally.
  • Only the final evaluation should be done on the test set.
• Set up validation to mimic train/test split.
  • In a competition, you need to identify the train/test split made by organizers.
  • In most cases, data is split by rows, time, groups or combined.
  • Logic of feature engineering depends on the data splitting strategy.

Credit

Validation stage

• We can observe that:
  • High deviation of the local CV scores.
• Possible causes:
  • Too little data.
  • Data is too diverse and inconsistent (e.g., December and January for store sales).
• Extensive validation techniques:
  • Perform k-fold split multiple times with different seeds, and average the scores.
  • Tune a model on one split, evaluate the model on the other.
• Following problems can be identified before the submission stage:
  • Different scores/optimal parameters between folds.
  • Public leaderboard score will be unreliable because of too little data.
  • Train and test data are from different distributions (using EDA).

Submission stage

• We can observe that:
  • LB score is consistently lower/higher than the local score:
  • LB score is not correlated with the local score.
• Possible causes:
  • We may already have a high variance of CV scores: calculate mean and std of CV scores and estimate if LB is expected.
  • Too little data in public leaderboard: trust your local validation.
  • Train and test are from different distributions: adjust distributions or perform leaderboard probing.
  • Overfitting
  • Incorrect cross-validation strategy
• Expect LB shuffle because of:
  • Randomness can shuffle scores on the private leaderboard.
  • Little amount of training or/and testing data.
  • Different public/private data or target distributions (e.g., time-based split).
• How to Select Your Final Models in a Kaggle Competition

Base models

• The following validation schemes are supposed to be used to estimate quality of the model.
• For getting test predictions don't forget to retrain your model using all training data.

Holdout

• Procedure (train_test_split):
  • Split train into two parts: trainA and trainB (usually 80/20).
  • Fit the model on trainA and validate it on trainB.
• Use holdout if scores on each fold are roughly the same.

K-Fold

• Procedure (KFold):
  • Split train into \(K\) folds.
  • Iterate though each fold:
    • Refit the model on all folds except the current one.
    • Validate the model on the current fold.
• Assumes that the samples are i.i.d.
• The performance measure reported by k-fold CV is the average of the values computed in the loop.
• Scores deviation in KFold can help to select statistically significant change in scores while tuning a model.
• The value of \(K\) being large could lead to low bias and high variance (overfitting).
• The advantage is that entire data is used for training and validation.
• For classification problems that exhibit a large imbalance (StratifiedKFold):
  • Stratified k-fold ensures that relative class frequencies are preserved in each train and validation fold.
• In this case we would like to know if a model generalizes well to the unseen groups (GroupKFold):
  • Group k-fold ensures that the same group is not represented in both testing and training sets.

LOO

• LOO is a k-fold scheme where \(K=N\) (LeaveOneOut).
• LOO often results in high variance as an estimator for the test error.
• 5-10 fold cross validation should be preferred to LOO.
• Mostly used for sparse datasets.

Time-based validation

• Procedure (TimeSeriesSplit):
  • Split train into chunks of duration \(T\). Select first \(M\) chunks.
  • Fit a model on these \(M\) chunks and predict for the chunk \(M+1\).
  • Then repeat this procedure for the next chunk and so on (imagine a moving window).
• Used if the samples have been generated using a time-dependent process.
• Time series data is characterised by the correlation between observations (autocorrelation).
• Does not assume that the samples are i.i.d.

Meta models

Simple holdout scheme

• Procedure:
  • Split train into three parts: trainA, trainB and trainC.
  • Fit \(N\) diverse models on trainA.
  • Predict for trainB, trainC, and test (getting meta-features trainB_meta, trainC_meta and test_meta).
  • Fit a meta-model on trainB_meta and validate it on trainC_meta.
  • When the meta-model is validated, fit it to [trainB_meta, trainC_meta] and predict for test_meta.
• This scheme is usually preferred over the other schemes if dataset is large.
• Fair validation scheme (validation set of meta-models not used in any way by base models)

Meta holdout scheme with OOF meta-features

• Procedure:
  • Split train into \(K\) folds.
  • Iterate though each fold:
    • Refit \(N\) diverse models on all folds except the current one.
    • Predict for the current fold.
    • For each object in train, we now have \(N\) meta-features (out-of-fold predictions, OOF) (getting train_meta)
  • Fit the models on train and predict for test (getting test_meta)
  • Split train_meta into two parts: train_metaA and train_metaB.
  • Fit a meta-model on train_metaA and validate it on train_metaB.
  • When the meta-model is validated, fit it to train_meta and predict for test_meta.

Meta KFold scheme with OOF meta-features

• Procedure:
  • Obtain OOF predictions for train_meta and test_meta.
  • Use KFold scheme on train_meta to validate the meta-model (with same seed as for OOF).
  • When the meta-model is validated, fit it to train_meta and predict for test_meta.

Holdout scheme with OOF meta-features

• Procedure:
  • Split train into two parts: trainA and trainB.
  • Fit models to trainA and predict for trainB (getting trainB_meta).
  • Obtain OOF predictions for trainA_meta.
  • Fit a meta-model to trainA_meta and validate on trainB_meta.
  • Obtain OOF predictions for train_meta and test_meta.
  • Fit the meta-model to train_meta and predict for test_meta.
• Fair validation scheme.

KFold scheme with OOF meta-features

• The same as holdout scheme with OOF meta-features but with \(K\) folds instead of trainA and trainB.
• This scheme gives the validation score with the least variance compared to the other schemes.
• But it is also the least efficient one from the computational perspective.
• Fair validation scheme.

KFold scheme in time series

• Procedure:
  • Obtain OOF meta-features using time-series split starting with \(M\) chunks.
  • Now we have meta-features for the chunks starting from \(M+1\) (getting train_meta).
  • Fit the models on train and predict for test (getting test_meta).
  • Perform time-series aware cross validation on meta-features.
  • Fit the meta-model to train_meta and predict for test_meta.

KFold scheme in time series with limited amount of data

• The same as meta KFold scheme with OOF meta-features but with respect to time.