Edit

Activation Functions

• How do we decide whether the neuron should fire or not?
• The activation function of a node maps the resulting values into the desired range.

Non-linearity

• Only nonlinear activation functions allow to compute nontrivial problems using only a small number of nodes, otherwise it would behave just like a single-layer perceptron.
• A multi-layered neural network can be regarded as a hierarchy of generalized linear models; according to this, activation functions are link functions, which in turn correspond to different distributional assumptions.

Credit

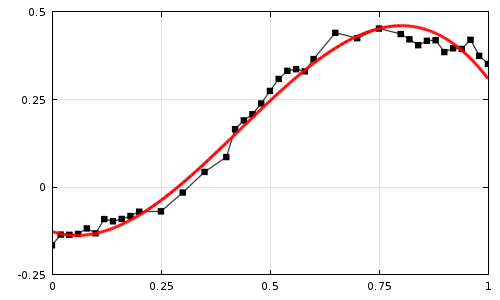
Comparison of different functions

• Use ReLu which should only be applied to the hidden layers. Be careful with your learning rates and possibly monitor the fraction of “dead” units in a network.
• If the model suffers form dead neurons during training then use leaky ReLu or Maxout function.
• Other functions are discouraged for vanilla feedforward implementation. They are more useful for recurrent networks, probabilistic models, and some autoencoders have additional requirements that rule out the use of piecewise linear activation functions.
• For output layers use a softmax function for a multi-class classification, and sigmoid or tanh function for a multi-label classification.
• In practice, the tanh non-linearity is always preferred to the sigmoid nonlinearity.
• Comparison of non-linear activation functions for deep neural networks on MNIST classification task (2018)

ReLU

$$\large{f(x)=\max{(0,x)}}$$

• The Rectified Linear Unit is simply thresholded at zero.
• Relu is like a switch for linearity. If you don't need it (\(x<0\)), you "switch" it off.

Pros

• Fewer vanishing gradient problems compared to sigmoidal activation functions that saturate in both directions. This arises when \(x>0\), where the gradient has a constant value.
• Sparse activation:
  • For example, in a randomly initialized network, only about 50% of hidden units are activated (having a non-zero output). This means less neurons are firing and the network is lighter and more robust to noise. Sparsity arises when \(x\leq{0}\)
• Efficient computation
• It was found to greatly accelerate the convergence of SGD compared to the sigmoid/tanh functions. It is argued that this is due to its linear, non-saturating form.
• Biological plausibility: One-sided, compared to the antisymmetry of tanh

Cons

• It should only be used within hidden layers.
• Non-differentiable at zero; however it is differentiable anywhere else, and a value of 0 or 1 can be chosen arbitrarily to fill the point where the input is 0.
• Dying ReLU problem: If the dot product of the input to a ReLU with its weights is negative, the output is 0. The gradient of \(max(x,0)\) is 0 when the output is 0. It may be mitigated by using leaky ReLU instead, which assign a small positive slope to the left of \(x=0\).
  • With a proper setting of the learning rate this is less frequently an issue.

$$\large{f(x)=\max{(0.1x,x)}}$$

Sparsity

• Inspiration from biology:
  • Biology appears to use a rule that says if the inputs sum to less than zero, don’t let the signal pass.
  • Also, studies conducted on ‘brain energy expenditure’ suggest that biological neurons encode information in a ‘sparse and distributed way‘. This means that the percentage of neurons that are active at the same time are very low (1–4%).
  • Ordinary artificial neural networks operate at much higher levels of activity and are less robust to small changes in input.
  • With the use of rectifying neurons we can achieve truly sparse representations.
• Effect on training:
  • Generalization: Dense representations can become strongly correlated during training, and this causes the network to overtrain because the "hidden information"
  • Makes internal representation linearly separable (think of Softmax classifier).
  • Sparse set is going to be more easily distributed because there are few interactions across the network. Credit
• Deep Sparse Rectifier Neural Networks

Maxout

$$\large{f(x)=\max{(w_1^Tx+b_1,w_2^Tx+b_2)}}$$

• The Maxout neuron generalizes the ReLU and its leaky version.
• where \(w\) and \(b\) are learnable parameters.
• An MLP with \(k=2\) maxout units can approximate any function. For ReLU we have \(𝑤1,𝑏1=0\).

Pros

• The Maxout neuron enjoys all the benefits of a ReLU unit (linear regime of operation, no saturation) and does not have its drawbacks (dying ReLU).

Cons

• However, unlike the ReLU neurons it doubles the number of bias parameters for every single neuron, leading to a high total number of parameters.

Sigmoid

$$\large{\sigma(x)=\frac{1}{1+e^{-x}}}$$

• Sigmoid (or logistic) function \(\sigma(x)\) is used for binary classification in logistic regression model.
• The sigmoid non-linearity takes a real-valued number and “squashes” it into range between 0 and 1.

Cons

• Saturates and kills gradients:
  • A very undesirable property of the sigmoid neuron is that when the neuron’s activation saturates at either tail of 0 or 1, the gradient at these regions is almost zero. Also, if the initial weights are too large then most neurons would become saturated and the network will barely learn.
• The derivative of the sigmoid maxes out at 0.25:
  • This means when you’re performing backpropagation with sigmoid units, the errors going back into the network will be shrunk by at least 75% at every layer. For layers close to the input layer, the weight updates will be tiny.
• Outputs are not zero-centered:
  • This could introduce undesirable zig-zagging dynamics in the gradient updates for the weights.
• Sigmoids have fallen out of favor as activations on hidden units.

Tanh

$$\large{\text{tanh}{(x)}=2\cdot\text{sigmoid}(2x)-1}$$

• The tanh non-linearity squashes a real-valued number to the range \([-1, 1]\).
• Tanh neuron is simply a scaled sigmoid neuron.

Pros

• Unlike the sigmoid neuron its output is zero-centered.

Softmax

$$\large{\sigma(x_j)=\frac{e^{x_j}}{\sum_i{e^{x_i}}}}$$

• While sigmoid function can only handle two classes, softmax can handle an arbitrary number of classes
• The output of the softmax function is equivalent to a categorical probability distribution, it tells you the probability that any of the classes are true.
• It transforms logits into probabilities. Logits simply means that the function operates on the unscaled output of earlier layers and that the relative scale to understand the units is linear.
• The calculated probabilities will be in the range of 0 to 1.
• The sum of all the probabilities is equals to 1.
• Softmax sums over the \(n\) different possible values of the class label
• It's exponential, can enlarge differences, and so pushes one result closer to 1 while another closer to 0.
• Softmax function is differentiable to train by gradient descent.

Cross-entropy loss

• We can't use MSE because our prediction function is non-linear. Squaring this prediction as we do in MSE results in a non-convex function with many local minimums. If our cost function has many local minimums, gradient descent may not find the optimal global minimum.
• Cross-entropy results in a convex loss function, of which the global minimum will be easy to find. Note that this is not necessarily the case anymore in multilayer neural networks.
• Cross entropy is often computed for output of softmax and true labels encoded in one hot encoding.
• What’s cool about using one-hot encoding for the label vector is that \(y_j\) is 0 except for the one true class.

Credit

• Softmax classification with cross-entropy