Edit

Hyperparameter Optimization

• Hyperparameters are model-specific properties that are not learned (as parameters) but fixed.
• Hyperparameter tuning is a meta-optimization task.
• Quality of the hyperparameters is not deterministic, as it depends on the outcome of a black box (the model training process).
  • We can't obtain the derivative and thus can't apply other mathematical optimization tools.
• Tuning the hyper-parameters of an estimator (sklearn)
• A list of open-source software

Best practices

• Select a subset of the most influential hyperparameters:
  • There are tons of hyperparameters and there is no time to tune them all.
  • Multiple comparisons problem: The more inferences are made, the more likely erroneous inferences are to occur, because of the sheer size of the parameter space to be searched.
• Understand exactly how they influence the training.
• Find out if the model is underfitting or overfitting.
• Use cross-validation to estimate the generalization performance.
• Don't spend too much time tuning hyperparameters.
  • Only if you have no more ideas or you have spare computational resources.
  • You cannot win competitions by tuning (but with features, hacks, leaks, and insights).
• It can take thousands of rounds for GBDT or neural networks to fit.
• Average everything:
  • Over random seed
  • Over small deviations from optimal parameters (e.g. average max_depth=3,4,5 for an optimal 5)

Grid search

• Try every combination of a preset list of hyper-parameters and evaluate the model for each combination.
• The list of combinations is calculated as a Cartesian product of different hyperparameter sets.
• Manually set bounds and discretization may be necessary before applying grid search.\
• Manual grid search:
  • Run a small grid, see if the optimum lies at either endpoint, and then expand the grid in that direction.
• Grid search is simple to set up and trivial to parallelize.
• It is the most expensive method in terms of total computation time.
• However, if run in parallel, it is fast in terms of wall clock time.
• Suffers from the curse of dimensionality.

Random search

• Random search only evaluates a random sample of points on the grid.
• This method is more efficient for parameter optimization than grid search.
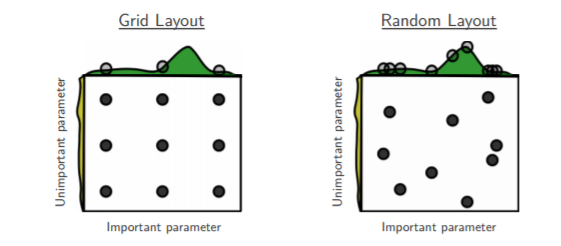
  • While grid search captures grid points only, random search is free to search the whole action space (without any aliasing). Credit
  • It is empirically and theoretically shown, that if at least 5% of the points on the grid yield a close-to-optimal solution, then random search with 60 trials will find that region with 95% probability (and the close-to-optimal region in stable machine learning models is quite large).
  • Compared to other methods it doesn't bog down in local optima.
  • Random search allows the inclusion of prior knowledge by specifying the distribution from which to sample.
• Works best when:
  • Only a small number of hyperparameters affects the final performance.
  • There are less number of dimensions.

Smart search

• The goal is to converge faster and make fewer evaluations.
• This type of methods is rarely parallelizable.
• Makes sense only if the evaluation procedure takes much longer than the sampling process.
• Smart search algorithms contain hyperparameters of their own.

Bayesian optimization

• Bayesian Optimization uses all of the information from previous evaluations and determines the next point to try.
• Builds a probabilistic model of the function mapping from the hyperparameters to the objective.

Credit

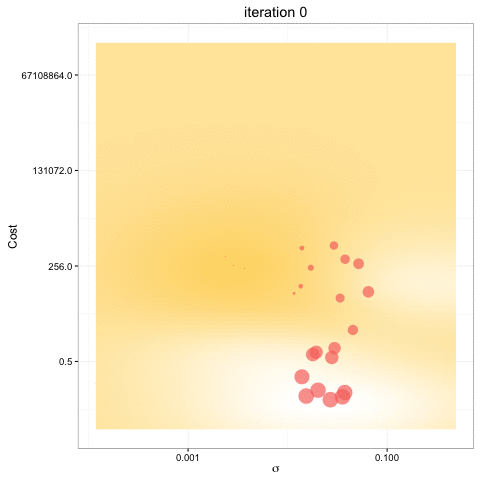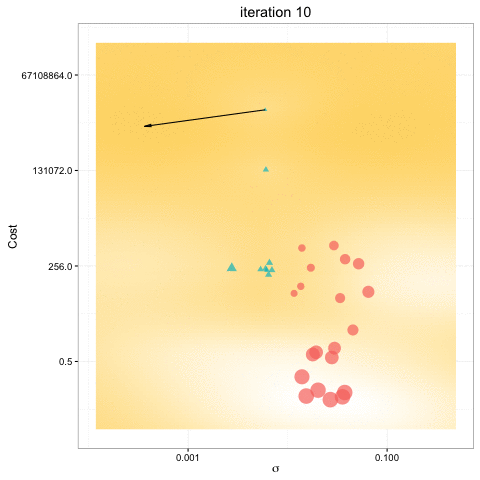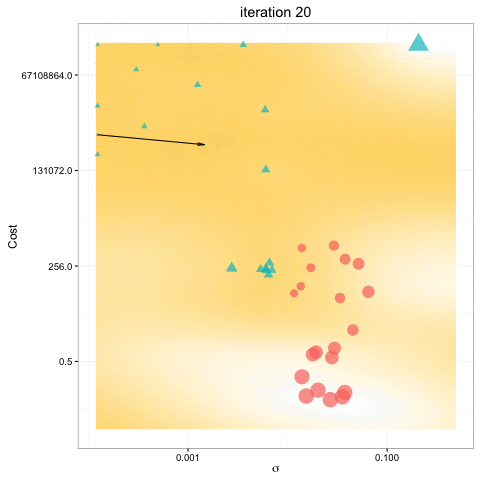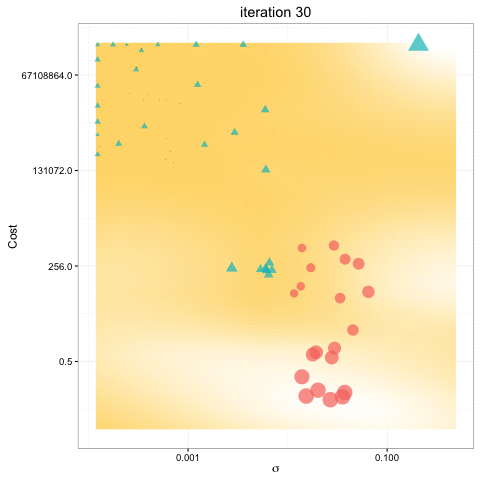
• Bayesian optimization obtain better results in fewer evaluations compared to grid search and random search.
• Bayesian optimization is much better than manual tuning.
• It is well suited for functions that are expensive to evaluate.
• Computes the mean and the variance.
• Function evaluation is cubic on the number of inputs.
  • Use a deterministic neural network with Bayesian linear regression on the last hidden layer.
  • Bayesian linear regression is much faster than Spearmint.
• Using Gaussian processes: Spearmint
• Using Tree-based Parzen Estimators: Hyperopt
  • Optimizing hyperparams with hyperopt

SMAC

• SMAC (Sequential Model-based Algorithm Configuration) trains a random forest of regression trees to approximate the response surface.
• This method may work better than Gaussian processes for categorical hyperparameters.
• Random forest tuning: SMAC

Derivative-free optimization

• Try a bunch of random points, approximate the gradient, and find the most likely search direction.
• Derivative-free methods include genetic algorithms and the Nelder-Mead method.
• Easy to implement and no less efficient that Bayesian optimization.
• Hyper gradient: hypergrad