datadocs

Edit

Metric Optimization

Tips

  • Why is my validation loss lower than my training loss?
    • Regularization applied during training, but not during validation/testing.
    • Training loss is measured during each epoch while validation loss is measured after each epoch.
    • The validation set may be easier than the training set.

Regression metrics

  • MSE, RMSE and R-squared are similar from the optimization perspective.
  • Do you have outliers (mistakes, measurement errors)? Use MAE
  • Do you have unexpected values you should care about? Use (R)MSE
  • MSPE and MAPE are sensitive to relative errors and can be thought as weighted versions of MSE and MAE, respectively.
    • Relative errors are intended to be both independent of scale and usable on all scales.
    • They are mainly used as forecast accuracy measures in time-series data.
    • A Survey of Forecast Error Measures

MSE-based metrics

MSE

$$\large{MSE=\frac{1}{n}\sum_{i=1}^{n}{(y_i-\hat{y}_i)^2}}$$

  • Mean Squared Error (MSE) measures the average squared difference between the estimated values and what is estimated.
  • Can range from 0 to \(\infty\) and are indifferent to the direction of errors.
  • It is a negatively-oriented score, which means lower values are better.
  • Useful if there are any unexpected values that we should care about.
  • MSE is one of the most widely used loss functions because of its ability to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
  • Limitations:
    • The least useful metric because of the lack of interpretability.
    • MSE has the disadvantage of heavily weighting outliers. $$MSE(30, 20)=100$$ $$MSE(30000, 20000)=100000000$$
    • Results in a particularly problematic behaviour if applied on noisy data: a single bad prediction may skew the metric towards underestimating the model's quality; if errors are smaller than one, the opposite effect takes place.
  • Best constant: mean
  • Loss function:
    • MSE can be directly optimized and is implemented by most libraries.
    • Synonyms: L2 Loss

RMSE

$$\large{RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(y_i-\hat{y}_i)^2}}}$$

  • Root Mean Square Error (RMSE) is introduced to make scale of the errors to be the same as the scale of targets.
  • Expresses average model prediction error in units of the variable of interest.
  • Every minimizer of MSE is also a minimizer for RMSE and vice versa, since the square root is an non-decreasing function.
  • Even though RMSE and MSE are similar in terms of optimization, they are not interchangeable for gradient-based methods: Travelling along RMSE gradient is equivalent to traveling along MSE gradient but with a different flowing rate.

(R)MSLE

$$\large{L(y,\hat{y})=\frac{1}{n}\sum_{i=0}^{n}{(\log{(y_i+1)}-\log{(\hat{y}_i+1)})^2}}$$

  • Mean Squared Logarithmic Error (MSLE) is MSE calculated on logarithmic scale.
  • The introduction of the logarithm makes MSLE only care about the relative difference between predictions and target.

$$MSLE(30, 20)=0.02861$$ $$MSLE(30000, 20000)=0.03100$$

  • Used in cases where the range of the target value is large (e.g., in forecasting).

  • The targets are usually non-negative but can equal to 0 - add a tiny constant before applying log.
  • RMSLE is considered as a better metric than MAPE, since it is less biased towards smaller targets.
  • Best constant: weighted mean in log space (weights are values themselves)
  • Loss function:
    • Transform target with \(z_i=\log{y_i+1}\)
    • Fit a model with MSE loss
    • Transform predictions back with \(\hat{y_i}=\exp{\hat{z_i}}-1\)

R squared

$$\large{R^2=1-\frac{SS_{\text{RES}}}{SS_{\text{TOT}}}=\frac{\sum_i{(y_i-\hat{y}_i)^2}}{\sum_i{(y_i-\overline{y}_i)^2}}}$$

  • The coefficient of determination, or \(R^2\) measures how much the model is better than the naive MSE baseline.
  • The MSE baseline can be thought of as the MSE that the simplest possible model would get.
  • Has the advantage of being scale-free (values between \(-\infty\) and \(1\)).
  • Values outside the range can occur when the model fits the data worse than the baseline.
  • Limitations:
    • R-squared cannot determine whether the coefficient estimates and predictions are biased.
    • Low values are not inherently bad for harder-to-predict data while high values do not necessarily indicate that the model has a good fit.
    • \(R^2\) will never decrease as variables are added and will probably experience an increase due to randomness. The adjusted R-squared can solve this by increasing only if the new term improves the model more than would be expected by chance.
  • Best constant: mean
  • Loss function:
    • RMSE or MSE loss should be used instead.

MAE-based metrics

MAE

$$\large{MAE=\frac{\sum_{i=1}^{n}{|y_i-\hat{y}_i|}}{n}}$$

  • MAE measures the average magnitude of the errors in a set of predictions, without considering their direction.
  • Expresses average model prediction error in units of the variable of interest.
  • Can range from 0 to \(\infty\) and are indifferent to the direction of errors.
  • It is a negatively-oriented score, which means lower values are better.
  • The individual differences are weighted equally.
  • MAE loss is useful if the training data is corrupted with outliers.
  • It is widely used in finance, where error 10 is exactly two times worse than error 5.
  • If the absolute value is not taken, the average error becomes the Mean Bias Error (MBE).
  • Best constant: median (more robust to outliers than mean)
  • Loss function:
    • MAE can be directly optimized but is implemented by fewer libraries.
    • Not differentable when predictions are equal to target (rare case)
    • One big problem in using MAE loss (for neural nets especially) is that its gradient will be large even for small loss values. Here helps a dynamic learning rate which decreases as we move closer to the minima.
    • MAE criterion is slower than MSE criterion
    • Synonyms: L1 Loss, Median regression

MAE vs. RMSE

  • RMSE has a tendency to be increasingly larger than MAE as the test sample size increases.
  • RMSE has the benefit of penalizing large errors more.
  • MAE is the most robust choice in respect to outliers.
  • MAE is shown to be an unbiased estimator while RMSE is a biased estimator.
  • Loss functions:
    • L1 loss is more robust to outliers, but its derivatives are not continuous, making it inefficient to find the solution.
    • L2 loss is sensitive to outliers, but gives a more stable and closed form solution (by setting its derivative to 0.)
    • Comparing the performance using L1 loss and L2 loss
    • As option: Huber loss combines good properties from both MSE and MAE.
    • As another option: Log-Cosh loss has all the advantages of Huber loss, and it’s twice differentiable everywhere (which is more favorable for models using Newton’s method), unlike Huber loss.
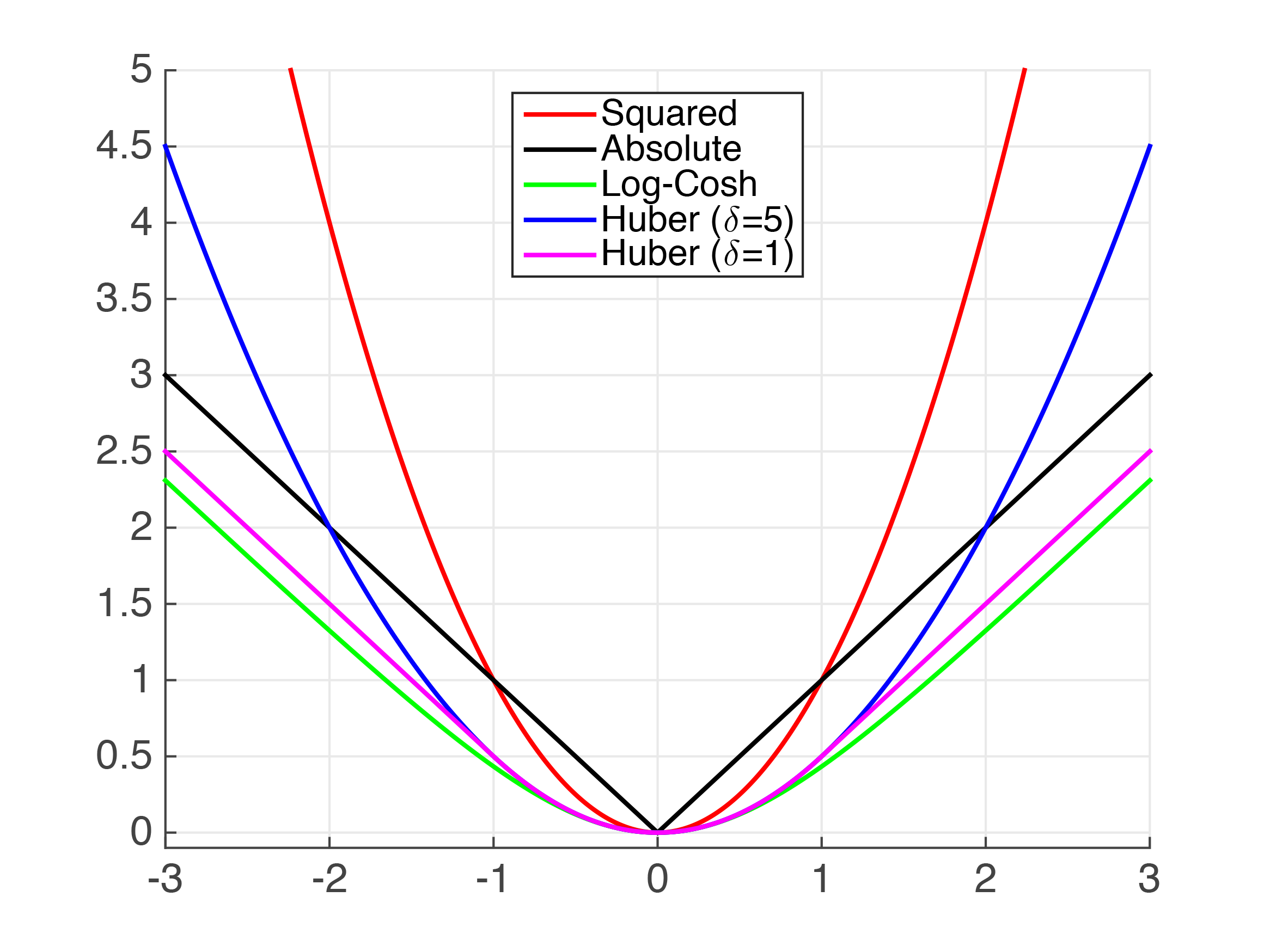
      Credit

MAPE

$$\large{MAPE=100\frac{1}{n}\sum_{i=1}^{n}{\frac{|y_i-\hat{y}_i|}{y_i}}}$$

  • Mean Absolute Percentage Error (MAPE) or Mean Absolute Deviation (MAD) is relative MAE (in %).
  • MAPE is often preferred because apparently managers understand percentages better than squared errors.
  • It is also commonly used as a loss function for regression problems and in model evaluation because of easy interpretation.
  • MAPEs greater than 100% can occur.
  • Limitations:
    • MAPE is biased towards smaller targets which yield higher errors.
    • MAPE can't be used for values where divisions and ratios make no sense (temperature scales).
    • RMSE method is more accurate and recent.
  • Best constant: weighted median
  • Loss function:
    • Use weights for samples (sample_weight) and optimize MAE.
    • Or resample the dataset beforehand (df.sample) and optimize MAE.
    • Usually need to resample many times and average.

Classification metrics

  • Logloss is the only metric that is easy to optimize directly.
  • For a binary classification task, fit any metric, and tune with the binarization threshold.
  • For multi-class tasks, fit any metric and tune parameters comparing the models by their accuracy score (not optimization metric).

Accuracy

$$\large{Accuracy=\frac{1}{n}\sum_{i=1}^{n}{[y_i=\hat{y}_i]}}$$

  • Accuracy is the ratio of number of correct predictions to the total number of input samples.
  • Works well for balanced datasets (one can get a nearly perfect score with imbalanced data classes).
  • To compute accuracy we need hard predictions, that is, apply a threshold.
  • The optimal threshold can be found with grid search.
  • Best constant: the most frequent class
  • Loss function:
    • The loss function is not differentable since gradients are zero almost always.
    • Zero-one loss may be approximated with a proxy loss such as logloss or Hinge loss.
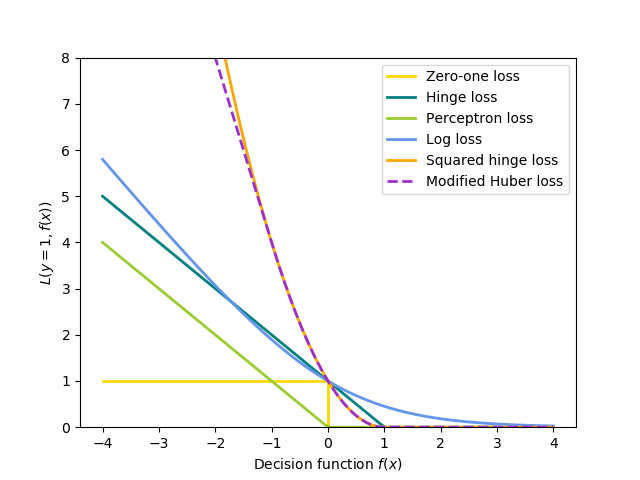
      Credit

Dealing with imbalanced data

  • Resampling:
    • Undersampling: sample from the majority class
    • Oversampling: replicate points from the minority class
    • Consider testing random and non-random (e.g., stratified) sampling schemes.
    • Consider testing different resampled ratios.
  • Generating synthetic data: create new synthetic points from the minority class or both classes (see SMOTE).
  • But information about class distribution is lost when resampling the dataset and can skew predictions on test.
  • Penalize mistakes on minority classes with class re-weighting (sample_weight).
  • Use a different performance metric (e.g., precision, recall, F-score, ROC AUC).
  • What metrics should be used for evaluating a model on an imbalanced data set?
  • Hands-on example: Detecting credit card fraud

LogLoss

$$\large{LogLoss=-\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}{y_{i,j}\log{\hat{y}_{i,j}}}}$$

  • Logarithmic loss, or logloss, increases as the predicted probability diverges from the actual label.
  • For all samples, enforces the model to assign a probability to be of a certain class.
  • To ensure numeric stability, predictions are clipped to be from \([10^{-15}, 1-10^{-15}]\) instead of \([0, 1]\).
  • Logloss has no upper bound (\([0, \infty)\)) with smaller values indicating a better fit.
  • Best constant: class frequency as vector
  • Loss function:
    • Logloss can be directly optimized and is implemented by most libraries.
    • NNs at default optimize logloss for classification.
    • Random forest classifiers are bad at logloss and produce rather conservative predictions. RFs can be calibrated in several ways: 1) Platt scaling (fit logistic regression to predictions), 2) isotonic regression, and 3) stacking.
    • Calibrated classifiers (rarely the case) will return posterior probabilities where threshold 0.5 would be optimal.

AUC

  • Area under the ROC Curve (AUC) of a classifier is a performance measurement for classification problem at various thresholds settings.
  • AUC tells how much model is capable of distinguishing between classes 0 and 1.

Credit

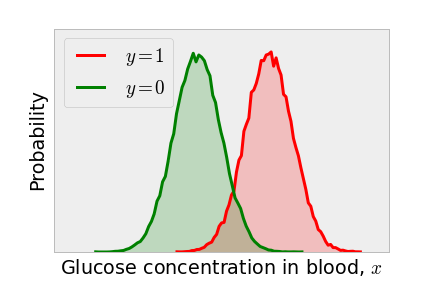
  • AUC is a rank-based metric (depends on ordering of predictions, not on absolute values)
  • Used for binary classification problems.
    • For multi-class tasks, we can plot \(N\) number of AUC-ROC curves for \(N\) number classes using one-vs-all methodology.
  • Good for cases when you need to estimate how well your model is at discriminating TRUE from FALSE values.
  • Removes the need for hard predictions and dependency on the threshold.
  • AUC can be obtained in different ways:
    • Area under the curve of plot FPR (\(\frac{TP}{TP+FN}\)) vs TPR (\(\frac{FP}{FP+TN}\)) at different points in \([0, 1]\) (Understanding ROC curves)
    • The probability of a pair of the predictions to be ordered in the right way.
    • The expectation that the classifier will rank a randomly chosen positive higher than a randomly chosen negative.
  • Best constant: any constant, random predictions lead to \(AUC=0.5\)
  • Loss function:
    • Although the loss function of AUC has zero gradients almost everywhere, exactly as accuracy loss, there exists an algorithm to optimize AUC with gradient-based methods, which use pair-wise loss instead of point-wise loss (supported by LGBM, XGBoost).
    • XGBoost learned with logloss gives a comparable AUC score.

Cohen's Kappa

$$\large{\kappa=1-\frac{1-p_{\text{observed}}}{1-p_{\text{chance}}}}$$

  • The kappa statistic is a metric that compares an observed accuracy with an expected accuracy (random chance). An accuracy of 80% is a lot more impressive with an expected accuracy of 50% versus an expected accuracy of 75%.
  • It is used not only to evaluate a single classifier, but also to evaluate classifiers amongst themselves.
  • Outputs 0 for baseline accuracy and 1 for excelent accuracy.
  • The more complex (and random) the dataset is, the lower kappa will be considered as high enough (such as 0.4)
  • Similar to how R squared better scales the MSE values for being easier explained.
  • Kappa is quite intuitive for medicine applications: how much the model agrees with professional doctors?
  • Best constant: the most frequent class
  • Loss function:
    • Treat this task as a regression problem (but more complex than MSE) and post-process the predictions by rounding them with a (tuned) threshold (if we relax the predictions to take values between the labels).
    • Or implement "soft kappa" loss

Ranking metrics

Clustering metrics

Last updated on 2019-10-15
← Advanced FeaturesValidation Schemes →