Edit

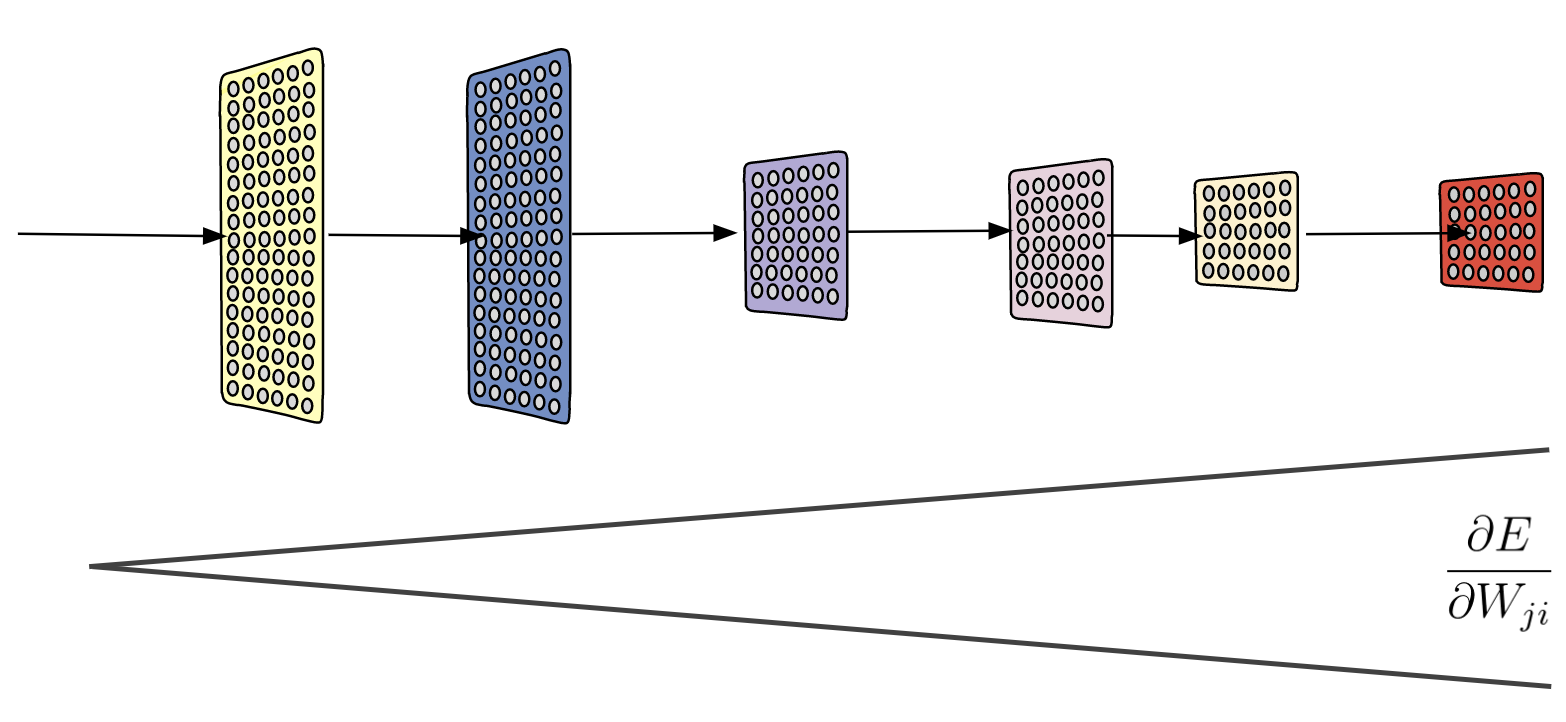
Backpropagation

• Backpropagation is an efficient method of computing gradients in directed graphs of computations.
• The backward propagation of error is a method used in ANNs to calculate a gradient that is needed in the calculation of the weights to be used in the network.
• An error is computed at the output and distributed backwards throughout the network’s layers.
• The weights are adjusted in proportion to their contribution to the total error.

Credit

• This is actually a simple implementation of chain rule of derivatives, which simply gives you the ability to compute all required partial derivatives in linear time in terms of the graph size.

Credit

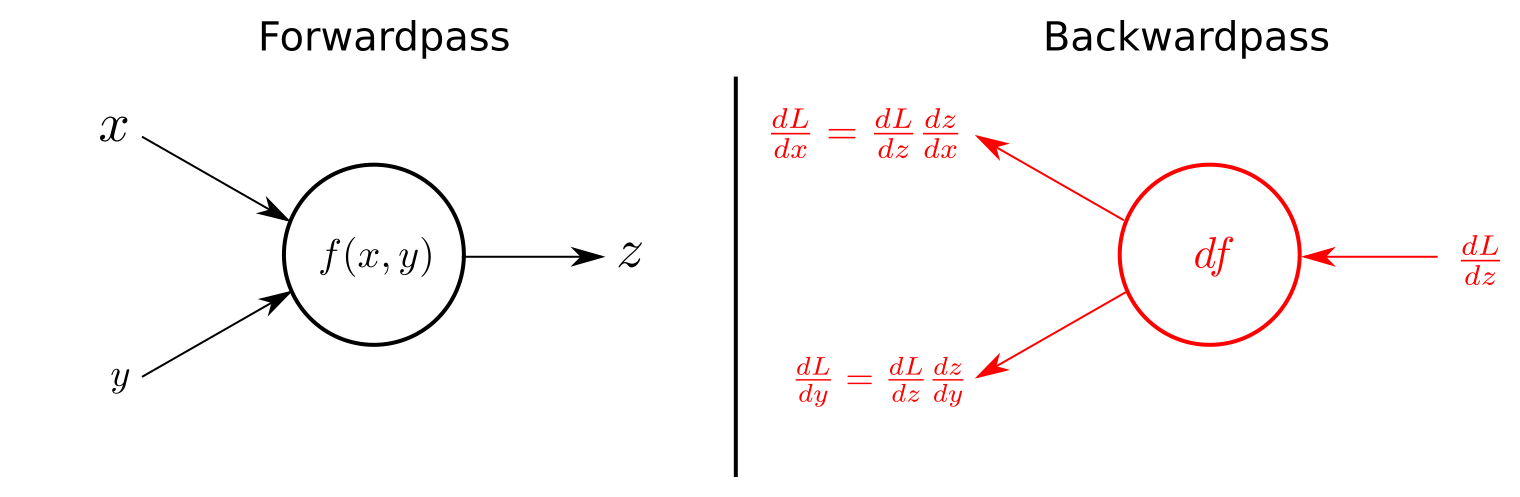
• In the context of learning, backpropagation is commonly used by the gradient descent optimization algorithm to adjust the weight of neurons by calculating the gradient of the loss function.
• Neural Networks: Feedforward and Backpropagation Explained & Optimization

Pros

• The backpropagation algorithm is more accurate and cheaper than estimating gradients numerically.

Best practices

• Backpropagation is computing gradients with respect to the cost, so anything in any layer that influences the ultimate cost should have a non-zero gradient.

Gradient checking

• Backpropagation is a notoriously difficult algorithm to debug and get right, especially since many subtly buggy implementations of it.
• It is very common and indeed arguably necessary to use centered finite difference approximations to check and debug your backpropagation calculations.
• Gradient checking verifies closeness between the gradients from backpropagation and the numerical approximation of the gradient (computed using forward propagation).
• Debugging: Gradient Checking

Procedure

• Use two-sided Taylor approximation which is 2x more precise than one-sided
• Assuming \(\epsilon=10^{−4}\), you’ll usually find that the left- and right-hand sides of the above will agree to at least 4 significant digits (and often many more).

$$\large{g(\theta)\approx\frac{J(\theta+\epsilon)-J(\theta-\epsilon)}{2\times\epsilon}}$$

where \(\theta\): model parameters, \(g\): gradients computed with backpropagation, \(J\): cost function computed with forward propagation

• If ever we are optimizing over several variables or over matrices, we can always pack these parameters into a long vector and use the same method here to check our derivatives. Then to check i-th parameter, increase/decrease i-th element of the vector by \(\epsilon\).

Best practices

• There’s a large range of values of \(\epsilon\) that should work well, but we don’t set \(\epsilon\) to be “extremely” small, say \(10^{−20}\), as that would lead to numerical roundoff errors.
• Gradient checking is slow, so we don't run it in every iteration of training. You would usually run it only to make sure your code is correct, then turn it off and use backprop for the actual learning process.
• Mostly gradient checking doesn't work with dropout.
• Be sure to disable gradient checking in testing phase.