Edit

Initialization

• For deep networks, we can use a heuristic to initialize the weights depending on the non-linear activation function.
• Paper on the selection of initialization and activation functions (2018)
• Usage of initializers

Zero initialization

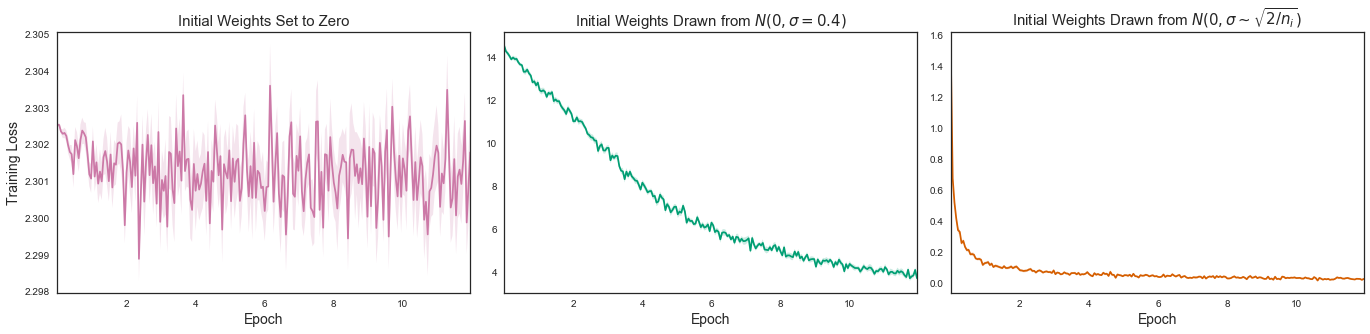
• Initializing weights to zero makes the hidden units symmetric and continues for all the iterations, which makes the model equivalent to a linear model.
• It is important to note that setting biases to 0 will not create any troubles as non-zero weights take care of breaking the symmetry.

Random initialization

• Generate random sample of weights from a Gaussian distribution having mean 0 and a standard deviation of 1.
• This serves the process of symmetry-breaking and gives much better accuracy.

Credit

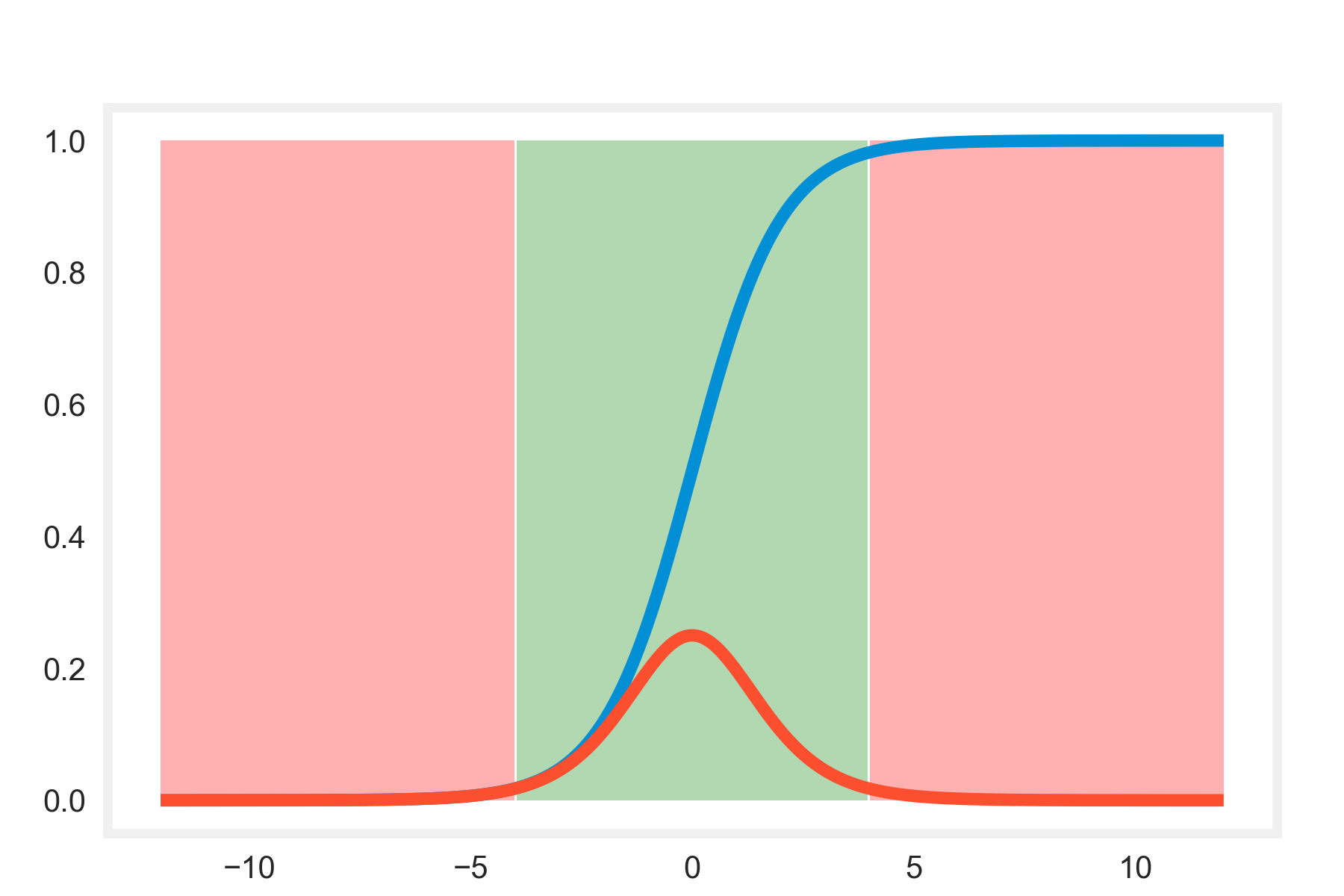
Vanishing gradients

• The weight update is minor and results in slower convergence:
  • This makes the optimization of the loss function slow.
  • In the worst case, this may completely stop the neural network from training further.
  • In case of sigmoid and tanh, if weights are large then the gradients will be vanishingly small.
• With ReLU vanishing gradients are generally not a problem.

Exploding gradients

• This may result in oscillating around the minima or even overshooting the optimum again and again and the model will never learn.
• Another impact of exploding gradients is that huge values of the gradients may cause number overflow resulting in incorrect computations or introductions of NaN’s.
  • This might also lead to the loss taking the value NaN.

Xavier initialization

• Xavier initialization method tries to initialize weights with a smarter value, such that neurons won’t start training in saturation.
• Draw random sample of weights from a Gaussian distribution with zero mean and variance:

$$\large{\sigma(w)=\sqrt{\frac{2}{n_{\text{in}}+n_{\text{out}}}}}$$

where \(n_{\text{in}}\): size of previous layer, \(n_{\text{out}}\): size of this layer

• Recent deep CNNs are mostly initialized by random weights drawn from Gaussian distributions.
• Xavier initialization makes sure the weights are "just right", keeping the signal in a reasonable range of values through many layers.
• The weights are still random but differ in range depending on the size of the previous layer of neurons.
• Helps in attaining a global minimum of the cost function faster and more efficiently.

Credit

• Likewise if using sigmoid/tanh activation function.
• Understanding the difficulty of training deep feedforward neural networks (2010)

He et al. initialization

• Draw random sample of weights from a truncated Gaussian distribution with zero mean and variance:

$$\large{\sigma(w)=\sqrt{\frac{2}{n_{\text{in}}}}}$$

• Likewise if using ReLu activation function.
• Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification (2015)