Neural Style Transfer

Neural style transfer (NST) is a technique used to generate images in the style of another image.
VGG network is more well-suited for NST than Inception.

Image optimization

A naive technique is to use an optimization technique starting off with a random noise image.
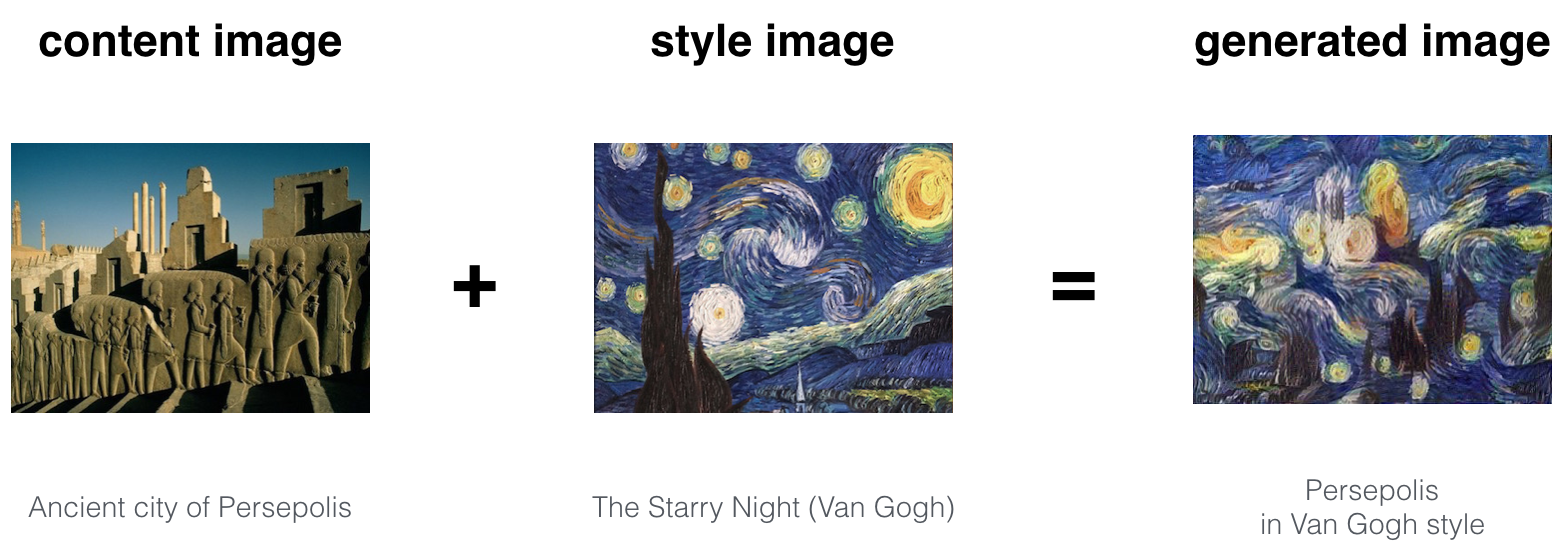
A better technique is to take three images: (1) a content image, (2) a style reference image (artwork), and (3) the input image to style. Blend them together such that the input image looks like the content image and "painted" like the style image.
CNNs have been learned to encode perceptual and semantic information, so they can be repurposed for the style transfer problem.

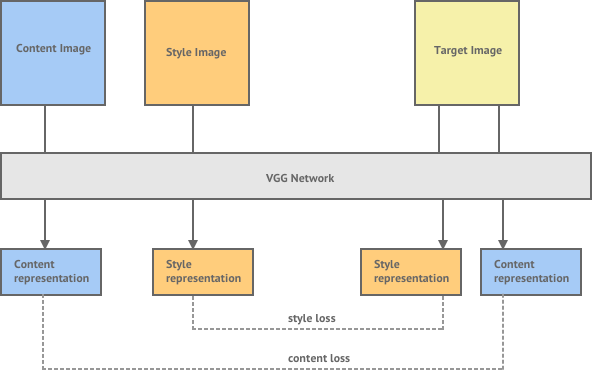
Use the outputs of various intermediate layers to compute two types of losses:
- style loss (how close is the pastiche to the style image in style)
- content loss (how close is the pastiche to the content image in content)
Those losses are then minimized by directly changing the pastiche image.
Losses are based not on per-pixel differences between images, but instead on more perceptual differences between them, which are captured in deeper layers.

The relative importance of these terms is determined by a set of scalar weights $\alpha$ and $\beta$.

$$\large{L_{\text{total}}(S,C,G)=\alpha L_{\text{content}}(C,G)+\beta L_{\text{style}}(S,G)}$$

Applying this to early layers results in finer textures whereas applying this to deeper layers capture smore higher-level elements of the image’s style.
The best results are achieved by a combination of many different layers from the network.

Pass both the pastiche image and the content image through some layers of the network and find the Euclidean distance between the intermediate representations of those images.

$$\large{L_{\text{content}}(C,G)=\frac{1}{2}\sum_{l}^L{\sum_{ij}{(C_{ij}-G_{ij})^2}}}$$

where $L$: number of layers

The style loss is the distance between the Gram matrices of the pastiche and style.
A Gram matrix results from multiplying a matrix with the transpose of itself.
The terms of the Gram matrix are proportional to the covariances of corresponding sets of features (channels), and thus captures information about which features tend to activate together.
By only capturing these aggregate statistics across the image, they are blind to the specific arrangement of objects inside the image. This is what allows them to capture information about style independent of content.

$$\large{L_{\text{GM}}(S,G,l)=\frac{1}{4N^2M^2}\sum_{ij}{(GM^S_{ij}-GM^G_{ij})^2}}$$

where $GM$: gram matrix, $N$: number of distinct feature maps, $M$: the width times the height of the feature map

There is also a possibility of assigning different weightages to the style loss at each layer.

$$\large{L_{\text{style}}(S,G)=\sum_{l}^{L}{w_l\cdot L_{GM}(S,G,l)}}$$

where $w_l$: weight for the layer $l$,